第13章 排序和搜索算法

• 排序
  • 11.1 冒泡排序
  • 11.2 选择排序
  • 11.3 插入排序
  • 11.4 合并排序
  • 11.5 快速排序

排序

11.1 冒泡排序

概念

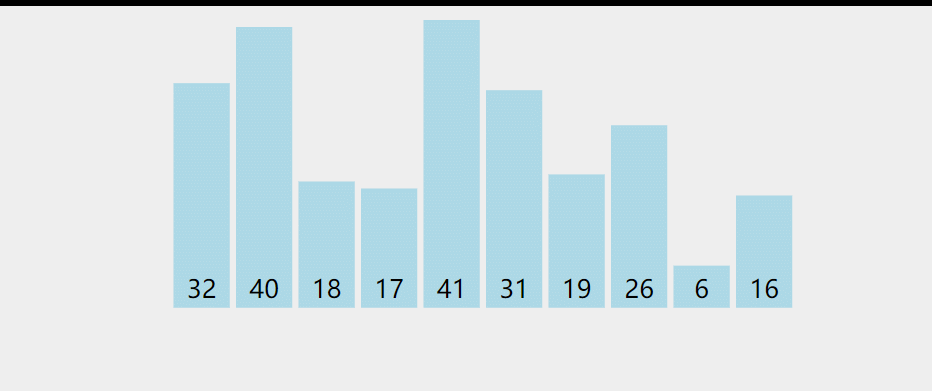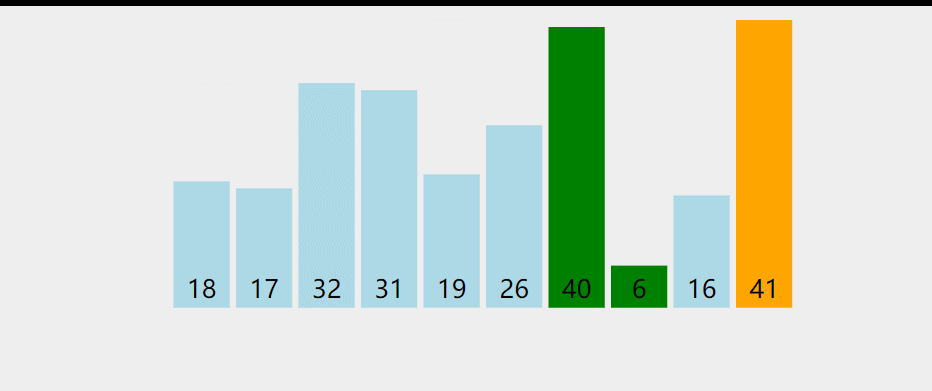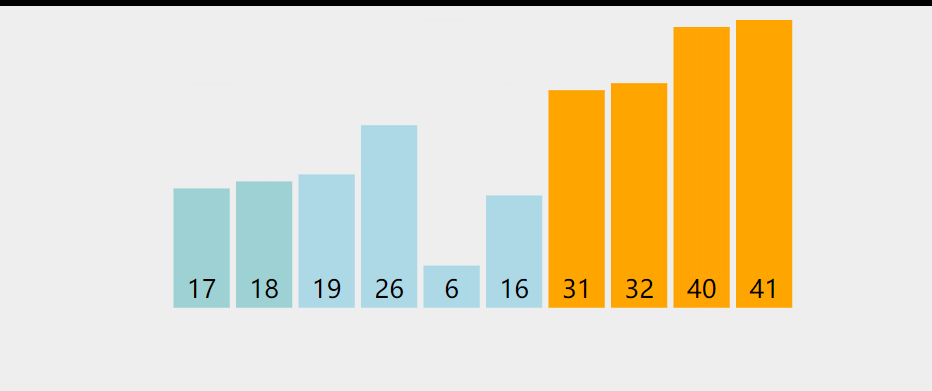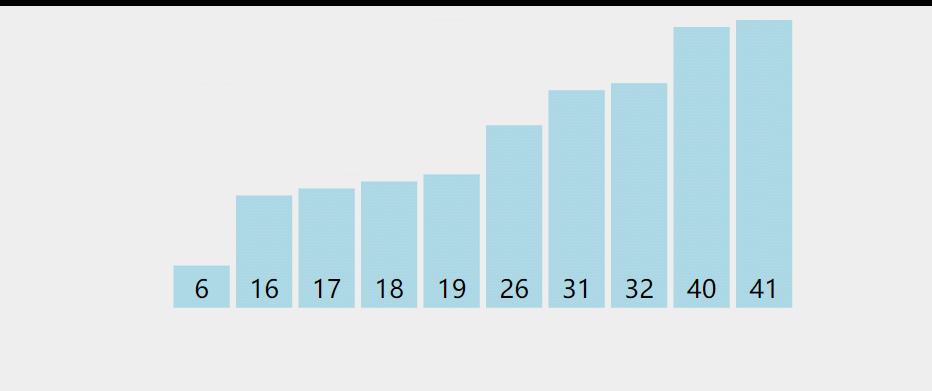
冒泡排序比较所有相邻的的两个项，如果第一个比第二个大，则交换它们。元素项向上移动至正确的顺序，就好像气泡升至表面一样。

实现

function bubbleSort(arr) {
  for (let i = 1; i < arr.length; i++) {
    for (let j = 0; j < arr.length - i; j++) {
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]
      }
    }
  }
}

复杂度

时间复杂度：O(n2)

空间复杂度：O(1)

稳定性

稳定

11.2 选择排序

概念

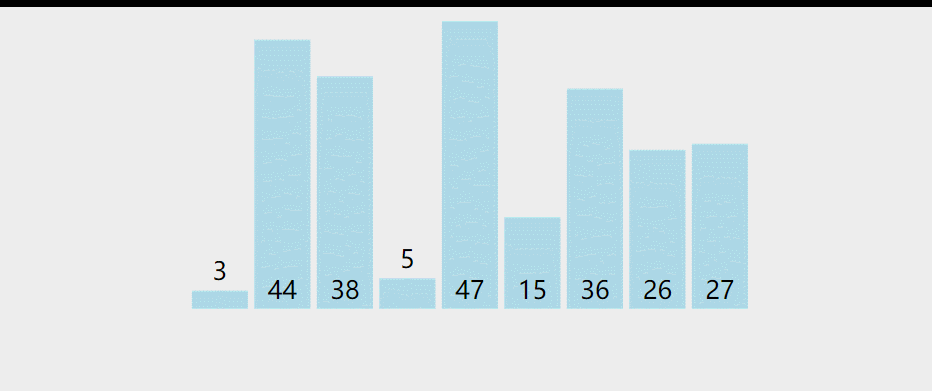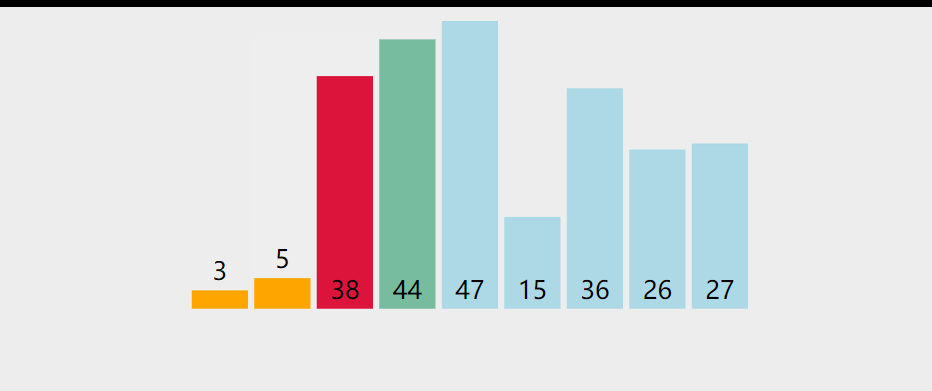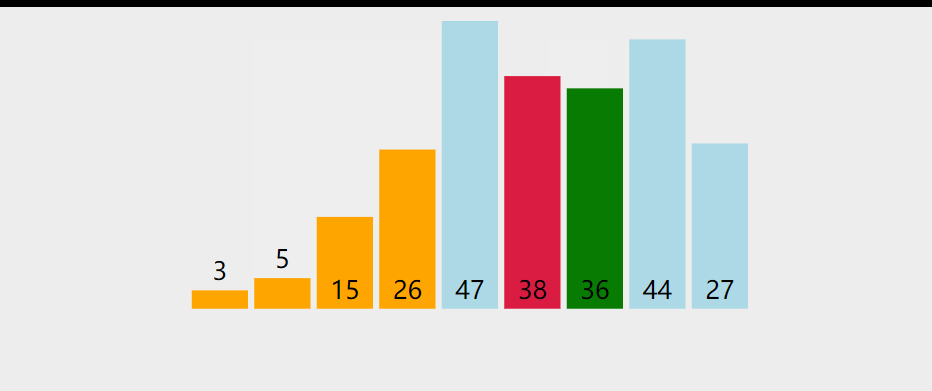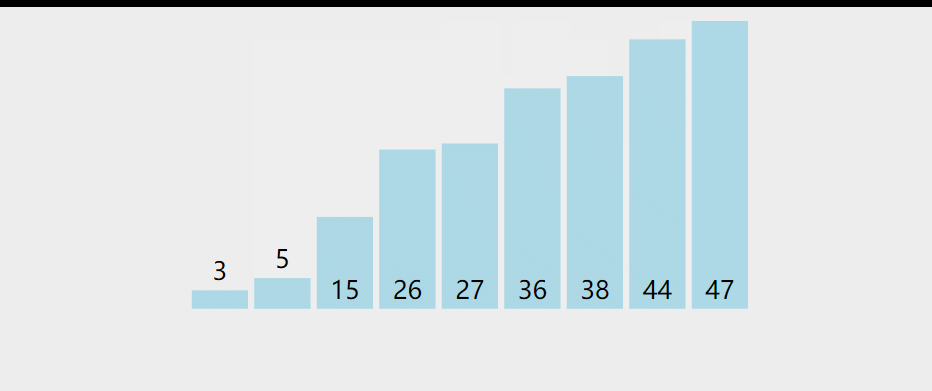
选择排序是一种原址比较排序算法。选择排序大致思路是找到数据结构中的最小值并将其放到第一位，接着找到第二小的值并放到第二位，以此类推。

实现

function selectionSort(arr) {
  for (let i = 0; i < arr.length - 1; i++) {
    let minIndex = i
    for (let j = i + 1; j < arr.length; j++) {
      if (arr[minIndex] > arr[j]) {
        minIndex = j
      }
    }
    if (minIndex !== i) {
      [arr[i], arr[minIndex]] = [arr[minIndex], arr[i]]
    }
  }
}

复杂度

时间复杂度：O(n2)

空间复杂度:O(1)

稳定性

不稳定

11.3 插入排序

概念

插入排序每次排一个数组项，以此方式构建最后的排序数组。假定第一项已经排序了。接着，它和第二项进行比较，第二项应该是待在原位还是插到第一项之前呢？这样，头两项就已经正确排序，接着和第三项比较，以此类推。

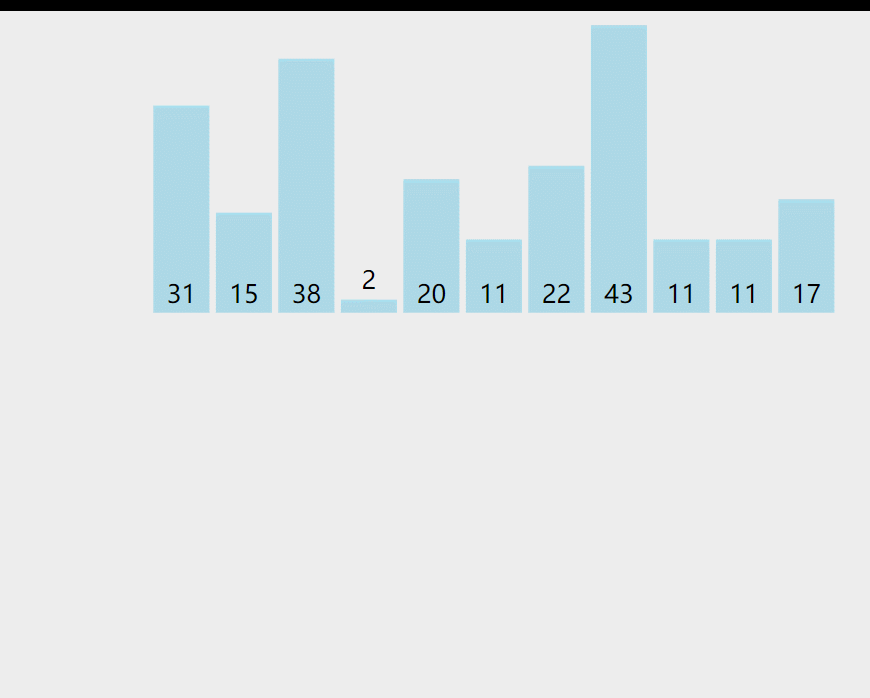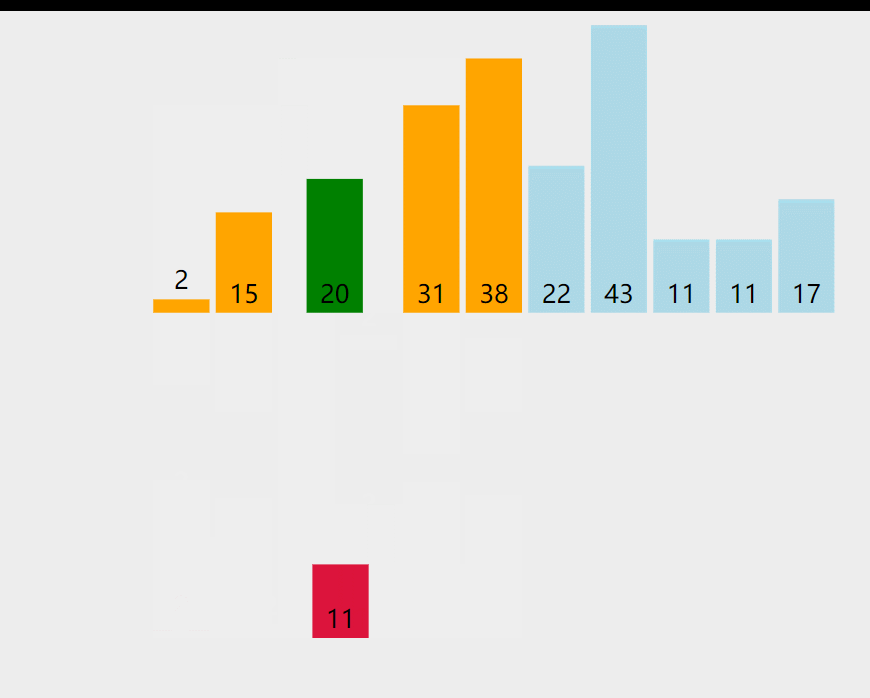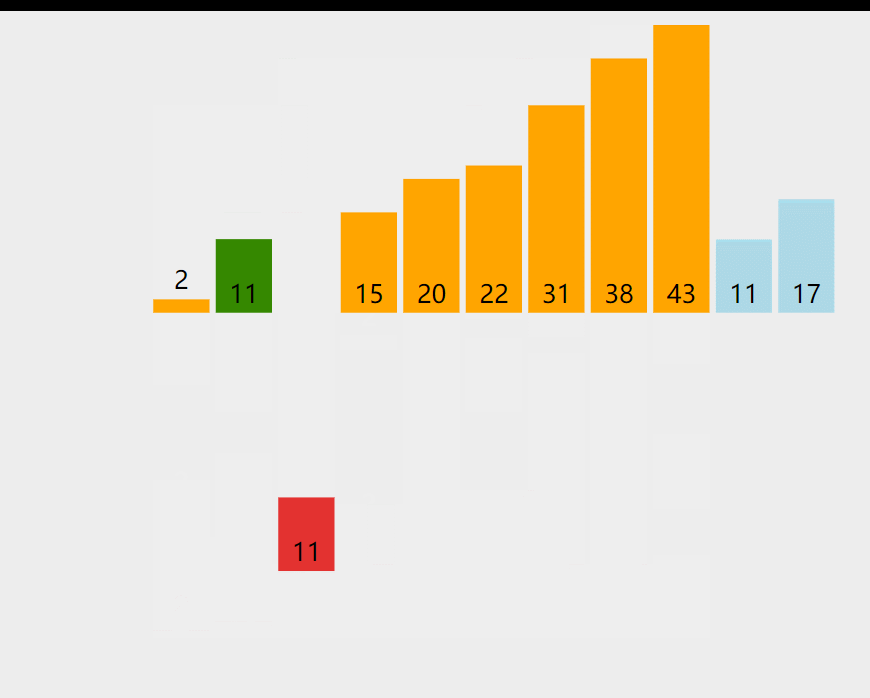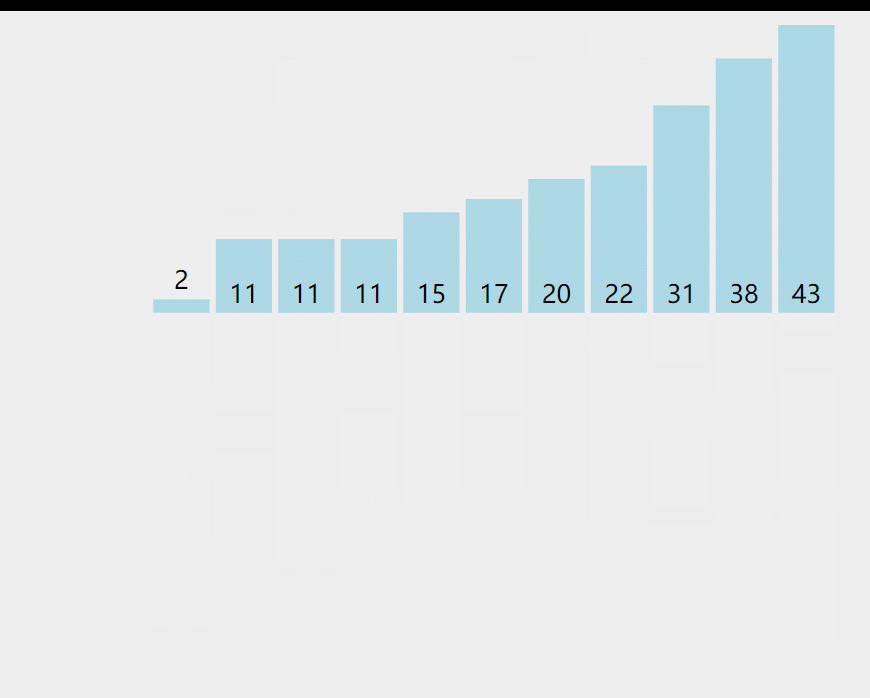
实现

function insertionSort(arr) {
  for (let i = 1; i < arr.length; i++) {
    let temp = arr[i]
    let j = i
    while (j > 0 && arr[j - 1] > temp) {
      arr[j] = arr[j - 1]
      j--
    }
    arr[j] = temp
  }
}

function insertionSort(arr) {
  for (let i = 1; i < arr.length; i++) {
    let curIndex = i
    while (curIndex > 0 && arr[curIndex - 1] > arr[curIndex]) {
      [arr[curIndex], arr[curIndex - 1]] = [arr[curIndex - 1], arr[curIndex]]
      curIndex--
    }
  }
}

复杂度

时间复杂度：O(n2)

空间复杂度:O(1)

稳定性

稳定

11.4 合并排序

概念

合并排序是一种分而治之算法。其思想是将原始数组切分成较小的数组，直到每个小数组只有一个位置，接着将小数组归并成较大的数组，直到最后只有一个排序完毕的大数组。

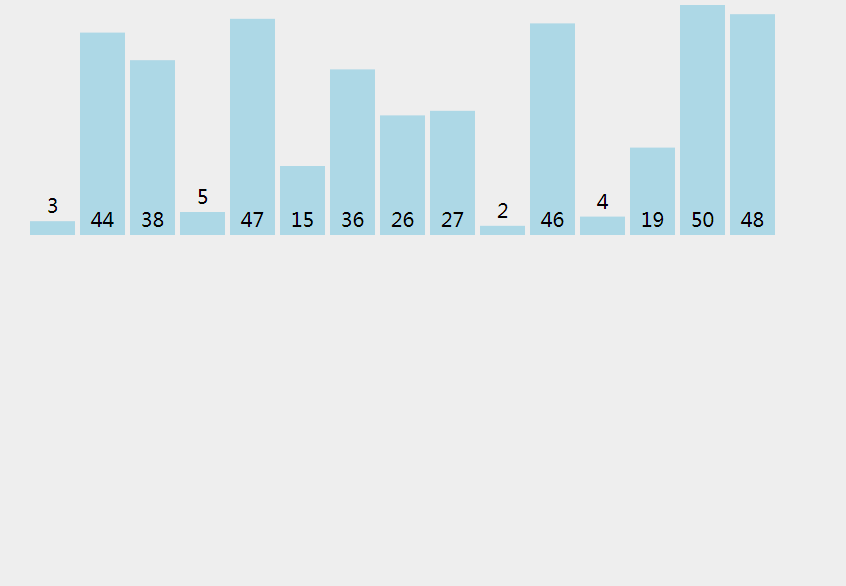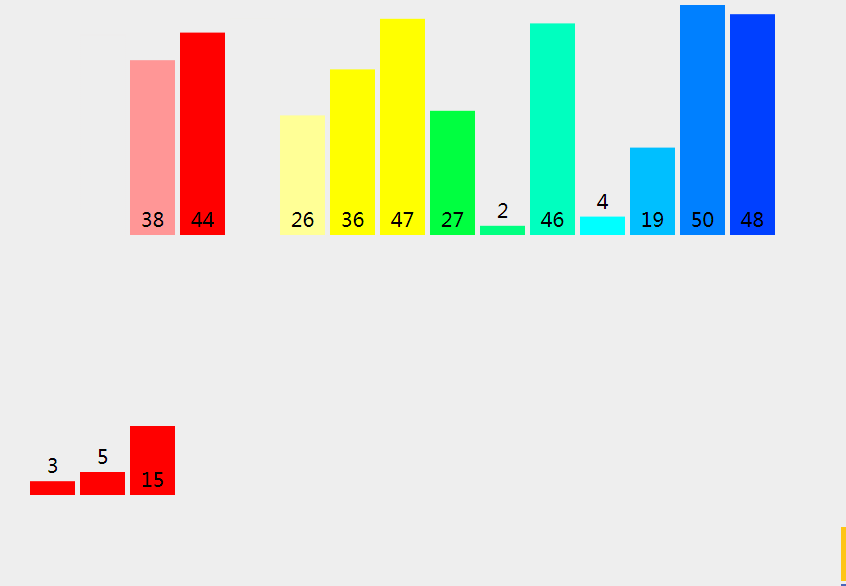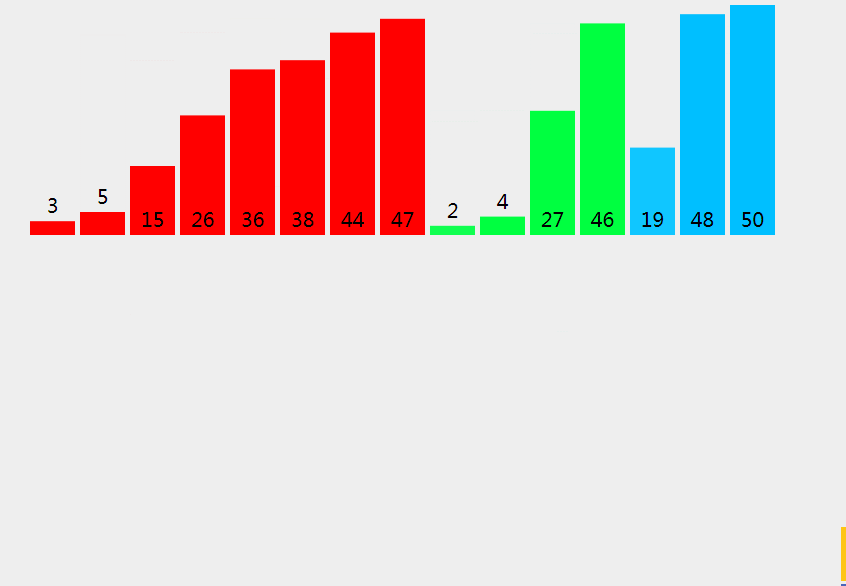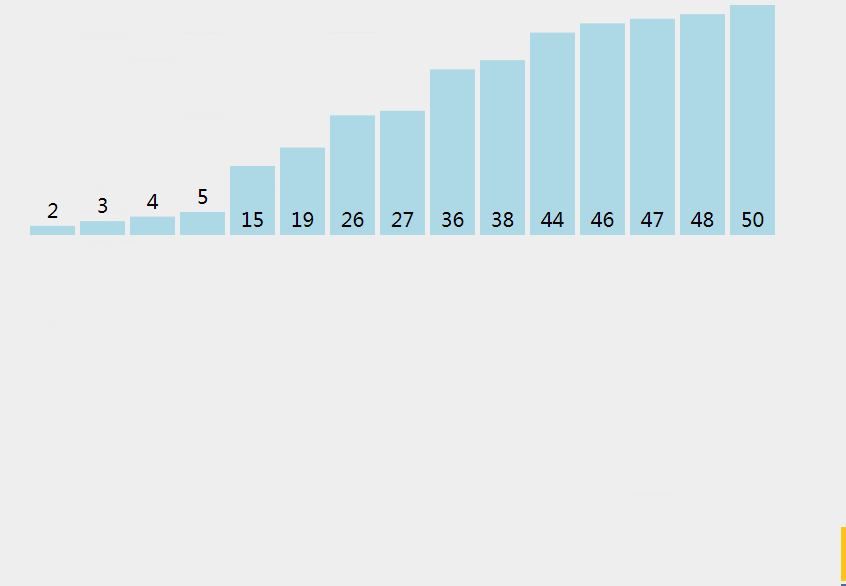
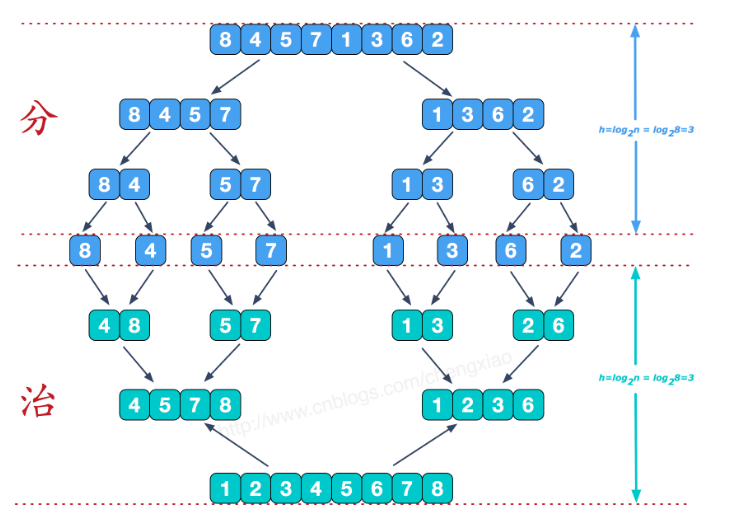
实现

/* 分散为小数组 */
function mergeSort(arr) {
  if(arr.length<2){
    return arr;
  }
  let mid=Math.floor(arr.length/2);
  let left=mergeSort(arr.slice(0,mid))
  let right=mergeSort(arr.slice(mid,arr.length))
  return merge(left,right)
}
/* 合并为大数组 */
function merge(left,right){
  let i=0;
  let j=0;
  let res=[];
  while(i<left.length&&j<right.length){
    if(left[i]>right[j]){
      res.push(right[j++])
    }else{
      res.push(left[i++]);
    }
  }
  return res.concat(i<left.length?left.slice(i):right.slice(j));
}

复杂度

时间复杂度:O(nlog(n))

空间复杂度:n

稳定性

稳定

11.5 快速排序

概念

快速排序：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据比另一部分的所有数据要小，再按这种方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，使整个数据变成有序序列。时间复杂度

实现步骤：

• 选择一个基准元素 target（一般选择第一个数）
• 将比 target 小的元素移动到数组左边，比 target 大的元素移动到数组右边
• 分别对 target 左侧和右侧的元素进行快速排序 从上面的步骤中我们可以看出，快速排序也利用了分治的思想（将问题分解成一些小问题递归求解）

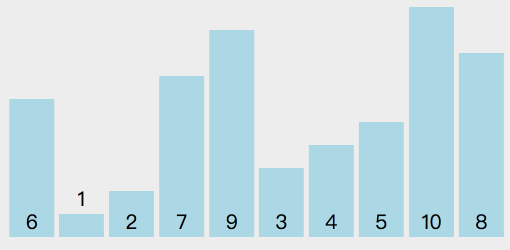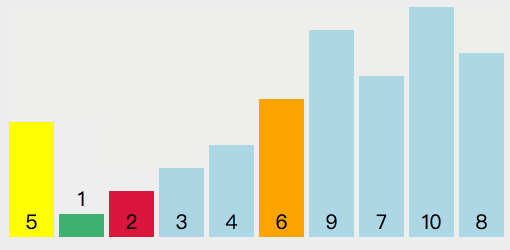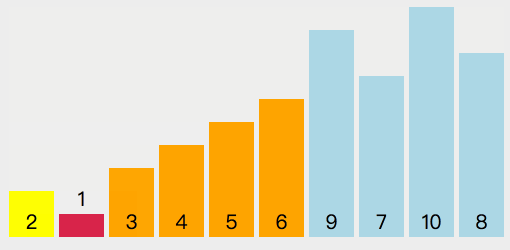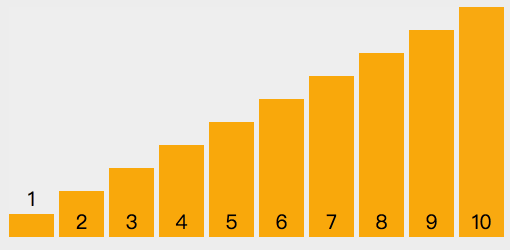
实现

方法一：递归（占额外存储空间、理解容易）

function quickSort(array) {
  if (array.length < 2) {
    return array;
  }
  const target = array[0];
  const left = [];
  const right = [];
  for (let i = 1; i < array.length; i++) {
    if (array[i] < target) {
      left.push(array[i]);
    } else {
      right.push(array[i]);
    }
  }
  return quickSort(left).concat([target], quickSort(right));
}

方法二：标准递归（不需要额外存储空间，写法思路稍复杂）

1. 首先从 arr 中选择中间值作为主元。
2. 创建 i,j。i 指向 arr 第一个值，j 指向 arr 最后一个值。移动 i 直到找到一个比主元大的值，移动 j 直到找到一个比主元小的值，然后交换它们，重复这个过程，直到 i 超过了 j。这个过程将使得比主元小的值都排在主元之前，比主元大的值都排在主元之后。
3. 对划分后的数组两个数组（比主元小的值组成的子数组，比主元大的值组成的子数组）重复之前两个步骤，直至数组完全排序。

function quickSort(arr, left, right) {
  if (arr.length < 2) return;
  left = left ? left : 0;
  right = right ? right : arr.length - 1;
  const pivot = arr[Math.floor((left + right) / 2)];
  let i = left;
  let j = right;
  while (i <= j) {
    while (arr[i] < pivot) {
      i++;
    }
    while (arr[j] > pivot) {
      j--;
    }
    if (i <= j) {
      [arr[i], arr[j]] = [arr[j], arr[i]];
      i++;
      j--;
    }
  }
  if (left < i - 1) {
    quickSort(arr, left, i - 1);
  }
  if (right > i) {
    quickSort(arr, i, right);
  }
  return arr;
}

方法三：非递归方法

function quickSort(arr, left, right) {
  left = left ? left : 0;
  right = right ? right : arr.length - 1;
  var stack = [];
  var pivot, i, j;
  stack.push(left);
  stack.push(right);

  while (stack.length) {
    j = right = stack.pop();
    i = left = stack.pop();
    pivot = arr[Math.floor((i + j) / 2)];
    while (i <= j) {
      while (arr[i] < pivot) {
        i++;
      }
      while (arr[j] > pivot) {
        j--;
      }
      if (i <= j) {
        [arr[i], arr[j]] = [arr[j], arr[i]];
        i++;
        j--;
      }
    }
    if (left < i - 1) {
      stack.push(left);
      stack.push(i - 1);
    }
    if (right > i) {
      stack.push(i);
      stack.push(right);
    }
  }
  return arr;
}

复杂度

时间复杂度：平均O(nlogn)，最坏O(n2)，实际上大多数情况下小于O(nlogn)

空间复杂度:O(logn)（递归调用消耗）

稳定性

不稳定